已知函数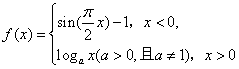 的图像上关于
的图像上关于![]() 轴对称的点至少有3对,则实数
轴对称的点至少有3对,则实数![]() 的取值范围是( )
的取值范围是( )
A. B.
B.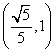 C.
C.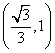 D.
D.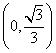
已知函数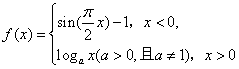 的图像上关于
的图像上关于![]() 轴对称的点至少有3对,则实数
轴对称的点至少有3对,则实数![]() 的取值范围是( )
的取值范围是( )
A. B.
B.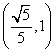 C.
C.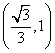 D.
D.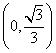
A
试题分析:原函数在![]() 轴左侧是一段正弦型函数图象,在
轴左侧是一段正弦型函数图象,在![]() 轴右侧是一条对数函数的图象
轴右侧是一条对数函数的图象
要使得图象上关于![]() 轴对称的点至少有
轴对称的点至少有![]() 对,可将左侧的图象对称到
对,可将左侧的图象对称到![]() 轴右侧,即
轴右侧,即![]() ,应该与原来
,应该与原来![]() 轴右侧的图象至少有
轴右侧的图象至少有![]() 个公共点,如图,
个公共点,如图,![]() 不能满足条件,只有
不能满足条件,只有![]()
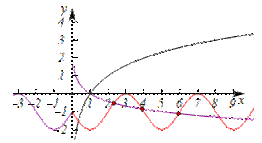
此时,只需在![]() 时,
时,![]() 的纵坐标大于
的纵坐标大于![]() ,即
,即![]() ,得
,得![]() ,故选A.
,故选A.
考点:1.分段函数;2.正弦型函数.
【方法点睛】依据题意将题目等价转化为函数![]()
![]() 与函数
与函数![]() ,
,![]() 至少有3个交点.显然两者联立无法求解(即无法从“数”上直接求解),所以利用数形结合直观的找到满足题意的条件即可.当
至少有3个交点.显然两者联立无法求解(即无法从“数”上直接求解),所以利用数形结合直观的找到满足题意的条件即可.当![]() 时,显然只有一个交点,当
时,显然只有一个交点,当![]() 时,找到至少有3个交点的“临界值”即可求解.本题使我们感受到等价转化思想的重要性,即如何将题目转化为熟知的题型和知识点上来,同时领略到了数形结合的魅力.
时,找到至少有3个交点的“临界值”即可求解.本题使我们感受到等价转化思想的重要性,即如何将题目转化为熟知的题型和知识点上来,同时领略到了数形结合的魅力.