如图，在矩形
中，
,将矩形绕点
按顺时针方向旋转得到矩形
，点
落在矩形的边
上，连接
，则的长是 .
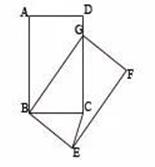
如图，在矩形中，,将矩形绕点按顺时针方向旋转得到矩形，点落在矩形的边上，连接，则的长是 .
.
【解析】
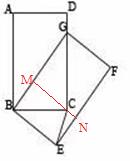
试题分析：如图，过点C作MN
BG，分别交BG、EF于点M、N，根据旋转的旋转可得AB=BG=EF=CD=5，AD=GF=3，在Rt△BCG中，根据勾股定理求得CG=4，再由
,即可求得CM=
,在Rt△BCM中，根据勾股定理求得BM=
，根据已知条件和辅助线作法易知四边形BENMW为矩形，根据矩形的旋转可得BE=MN=3,BM=EN=
,所以CN=MN-CM=3-=
,在Rt△ECN中，根据勾股定理求得EC=
.
考点：四边形与旋转的综合题.