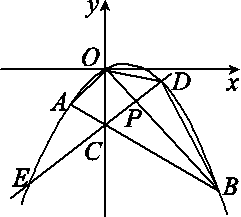
如图，在平面直角坐标系中，点A的坐标为(m，m)，点B的坐标为(n，－n)，抛物线经过A，O，B三点，连接OA，OB，AB，线段AB交y轴于点C.已知实数m，n(m<n)是方程
的两根．
(1)求抛物线的解析式．
(2)若P为线段OB上的一个动点(不与点O，B重合)，直线PC与抛物线交于D，E两点(点D在y轴右侧)，连接OD，BD.
①当△OPC为等腰三角形时，求点P的坐标；
②求△BOD面积的最大值，并写出此时点D的坐标．
如图，在平面直角坐标系中，点A的坐标为(m，m)，点B的坐标为(n，－n)，抛物线经过A，O，B三点，连接OA，OB，AB，线段AB交y轴于点C.已知实数m，n(m<n)是方程的两根．
(1)求抛物线的解析式．
(2)若P为线段OB上的一个动点(不与点O，B重合)，直线PC与抛物线交于D，E两点(点D在y轴右侧)，连接OD，BD.
①当△OPC为等腰三角形时，求点P的坐标；
②求△BOD面积的最大值，并写出此时点D的坐标．
解：(1)解方程x2－2x－3＝0，得x1＝3，x2＝－1.
∵m＜n，∴m＝－1，n＝3.
∴A(－1，－1)，B(3，－3)． …………（2分）
∵抛物线过原点，
∴可设抛物线的解析式为y＝ax2＋bx，得
解得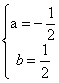
∴抛物线的解析式为y＝－
x2＋x. …………（4分）
(2)①设直线AB的解析式为y＝kx＋b，根据题意，得
解得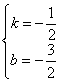
∴直线AB的解析式为y＝－x－
， …………（5分）
∴C(0，－)．
又∵直线OB的解析式为y＝－x，
故设P(x，－x)． …………………（6分）
∵△OPC为等腰三角形，则
Ⅰ)当OC＝OP时，x2＋(－x)2＝
，
解得x1＝
，x2＝－(舍去)，
∴P1(，－)．
(Ⅱ)当PO＝PC时，x2＋(－x)2＝x2＋(x－)2，
解得x＝
，
∴P2(，－)．
(Ⅲ)当OC＝PC时，x2＋(x－)2＝，
解得x1＝，x2＝0(舍去)，
∴P3(，－)．
综上所述，点P的坐标为(，－)或(，－)或(，－)． ……（9分）
②设D(x，y)(x＞0)．
分别过点D，B作DG⊥y轴于点G，BF⊥y轴于点F，
则G(0，y)，F(0，－3)，
∴S△BOD＝SRt△ODG＋S梯形DGFB－SRt△OBF
＝x×(－y)＋(x＋3)×(3＋y)－×3×3
＝－xy＋x＋xy＋
＋y－
＝y＋x.
又∵y＝－x2＋x，
∴S△BOD＝－x2＋x＝－(x－)2＋
. …………（11分）
∵0＜x＜3，
∴当x＝时，S△BOD的最大值为，
此时D(，－
)．