如图，四边形ABCO为矩形，点A在x轴上，点C在y轴上，且点B的坐标为（﹣1，2），将此矩形绕点O顺时针旋转90°得矩形DEFO，抛物线y=﹣x2+bx+c过B，E两点．
（1）求此抛物线的函数关系式．
（2）将矩形ABCO向左平移，并且使此矩形的中心在此抛物线上，求平移距离．
（3）将矩形DEFO向上平移距离d，并且使此抛物线的顶点在此矩形的边上，则d的值是 ．
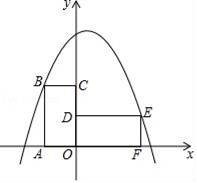
如图，四边形ABCO为矩形，点A在x轴上，点C在y轴上，且点B的坐标为（﹣1，2），将此矩形绕点O顺时针旋转90°得矩形DEFO，抛物线y=﹣x2+bx+c过B，E两点．
（1）求此抛物线的函数关系式．
（2）将矩形ABCO向左平移，并且使此矩形的中心在此抛物线上，求平移距离．
（3）将矩形DEFO向上平移距离d，并且使此抛物线的顶点在此矩形的边上，则d的值是 ．
【考点】二次函数图象与几何变换．
【分析】（1）待定系数法即可解决问题．
（2）矩形ABCO的中心坐标为（﹣
，1），可得1=﹣x2+
x+
，解得x=﹣
或2，所以平移距离d=﹣﹣（﹣）=
．
（3）求出顶点坐标，点E坐标，即可解决问题．
【解答】解：（1）由题意，点E的坐标为（2，1），
则
，解得
，
∴此抛物线的解析式为y=﹣x2+x+．
（2）∵矩形ABCO的中心坐标为（﹣，1），
∴1=﹣x2+x+，
解得x=﹣或2，
∴平移距离d=﹣
﹣（﹣
）=
．
（3）∵y=﹣x2+
x+
=﹣（x﹣
）2+
，
∴抛物线的顶点坐标为（，），
∵E（2，1），
∴平移距离d=或﹣1=
，
故答案为或．