如图，已知△ABC中，AB=AC=12cm，BC=10cm，点D为AB的中点。如果点P在线段

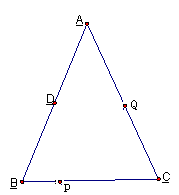
如图，已知△ABC中，AB=AC=12cm，BC=10cm，点D为AB的中点。如果点P在线段BC上以2cm／s的速度由点B向C点运动，同时，点Q在线段AC 上由点A向C点以4cm／s的速度运动。

(1)、若点P、Q两点分别从B、A 两点同时出发，经过2秒后，△BPD与△CQP是否全等，请说明理由。

（2）、若点P、Q两点分别从B、A 两点同时出发，△CPQ的周长为18cm，问：经过几秒后，△CPQ是等腰三角形？

 解：（1），△BPD与△CQP是全等。理由如下： 

当P，Q两点分别从B，A两点同时出发运动2秒时

有BP=2×2=4cm，AQ=4×2=8cm      

则CP=BC-BP=10-4=6cm

  CQ=AC-AQ=12-8=4cm         

∵D是AB的中点

∴BD=1/2AB=1/2×12=6cm

∴BP=CQ， BD=CP            

          又∵△ABC中，AB=AC

            ∴∠B=∠C                   

            在△BPD和△CQP中

              BP=CQ

              ∠B=∠C

              BD=CP

∴△BPD≌△CQP(SAS)        

   (2)设当P，Q两点同时出发运动t秒时，

      有BP=2t，AQ=4t  ∴t的取值范围为0﹤t≤3

      则CP=10-2t，CQ=12-4t           

      ∵△CPQ的周长为18cm，

      ∴PQ=18-(10-2t)-( 12-4t)=6t-4  

      要使△CPQ是等腰三角形，则可分为三种情况讨论：

①     当CP=CQ时，则有10-2t=12-4t

                  解得：t=1    

②     当PQ=PC时，则有6t-4=10-2t

                  解得：t=   

③     当QP=QC时，则有6t-4=12-4t

                  解得：t=  

三种情况均符合t的取值范围。

    综上所述，经过1秒或秒或秒时，△CPQ是等腰三角形