如图，在△ABC中，AB=AC，D为直线BC上一动点（不与点B，C重合），在AD

如图，在△ABC中，AB=AC，D为直线BC上一动点（不与点B，C重合），在AD的右侧作△ACE，使得AE=AD，∠DAE=∠BAC，连接CE．

（1）当D在线段上时．

①求证：．

②请判断点D在何处时，，并说明理由．

（2）当时，若中最小角为28°，求的度数．

（1）①证明见解析；②D运动到BC中点时，AC⊥DE；（2）28°或32°或92°．

【解析】

【分析】

（1）①根据SAS即可证明；②D运动到BC中点时，AC⊥DE；利用等腰三角形的三线合一即可证明；

（2）分三种情形分别求解即可解决问题．

【详解】

（1）①∵∠DAE=∠BAC，∴∠BAD=∠CAE，

在△BAD和△CAE中，∵，

∴△BAD≌△CAE．

②D运动到BC中点时，AC⊥DE．理由如下：

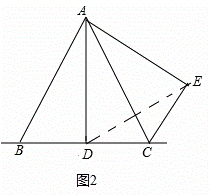
如图2，连接DE．

∵AB=AC，BD=CD，∴AD⊥BC，∠BAD=∠CAD．

∵∠BAD=∠CAE，∴∠CAD=∠CAE．

∵AD=AE，∴AC⊥DE．

（2）∠ADB的度数为28°或32°或92°．

理由：①如图3①中，当点D在CB的延长线上时．

∵CE∥AB，∴∠BAE=∠AEC，∠BCE=∠ABC．

∵△DAB≌△EAC，∴∠ADB=∠AEC，∠ABD=∠ACE，∴∠BAC=∠BAE+EAC=∠AEC+∠EAC=180°﹣∠ACE=180°﹣∠ABD=∠ABC=∠ACB，∴△ABC是等边三角形．

此时∠ADB或∠BAD可为最小角28°，

∴∠ADB=∠ABC﹣∠BAD=32°或∠ADB=28°．

②当点D在线段BC上时，同理可证△BAD≌△CAE，∴∠ABD=∠ACE．

∵CE∥AB，∴∠BAC=∠ACE=∠ABC，∴△ABC为等边三角形，∴∠ABD=60°，此时最小角只能是∠DAB=28°，此时∠ADB=180°﹣28°﹣60°=92°．

③当点D在BC 延长线上时，同理△BAD≌△CAE，∠BAC=∠ACE=∠ABC，

∴△ABC为等边三角形，∠BAD=∠CAE，AD=AE．

∵∠BAC=∠DAE=60°，∴△ADE为等边三角形．

此时△ABD中，最小角只能是∠ADB=28°．

综上所述：满足条件的∠ABD的值为28°或32°或92°．

【点睛】

本题考查了三角形综合题、等腰三角形的性质、全等三角形的判定和性质、等边三角形的判定与性质等知识，解题的关键是准确寻找全等三角形解决问题，学会用分类讨论的首先思考问题，属于中考压轴题．