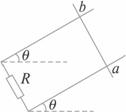
图1-5
(1)求金属棒沿导轨由静止开始下滑时的加速度大小;
(2)当金属棒下滑速度达到稳定时,电阻R消耗的功率为8 W,求该速度的大小;
(3)在上问中,若R=2 Ω,金属棒中的电流方向由a到b,求磁感应强度的大小与方向.
(g=

图1-5
(1)求金属棒沿导轨由静止开始下滑时的加速度大小;
(2)当金属棒下滑速度达到稳定时,电阻R消耗的功率为8 W,求该速度的大小;
(3)在上问中,若R=2 Ω,金属棒中的电流方向由a到b,求磁感应强度的大小与方向.
(g=
解:(1)金属棒开始下滑的初速度为零,根据牛顿第二定律
mgsinθ-μmgcosθ=ma
由上式解得a=10×(0.6-0.25×0.8) m/s2=
(2)设金属棒运动达到稳定时,速度为v,所受安培力为F,棒在沿导轨方向受力平衡mgsinθ-μmgcosθ-F=0
此时金属棒克服安培力做功的功率等于电路中电阻R消耗的电功率Fv=P
由上述两式解得v=![]() m/s=
m/s=
(3)设电路中电流为I,两导轨间金属棒的长为l,磁场的磁感应强度为B
则I=![]()
P=I2R
解得B=![]() ×1 T=0.4 T
×1 T=0.4 T
磁场方向垂直导轨平面向上.