设函数
，
.
（Ⅰ）当
时，函数
与
在
处的切线互相垂直，求
的值；
（Ⅱ）若函数
在定义域内不单调，求
的取值范围；
（Ⅲ）是否存在实数
,使得
对任意正实数
恒成立？若存在，求出满足条件的实数；若不存在，请说明理由.
设函数，.
（Ⅰ）当时，函数与在处的切线互相垂直，求的值；
（Ⅱ）若函数在定义域内不单调，求的取值范围；
（Ⅲ）是否存在实数,使得对任意正实数恒成立？若存在，求出满足条件的实数；若不存在，请说明理由.
【解析】（Ⅰ）当时，
，∴在处的切线斜率
，由
，∴
， ∴
，∴
.
（Ⅱ）易知函数的定义域为
，
又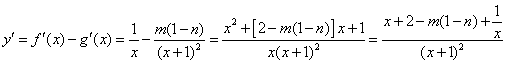
，
由题意
，得
的最小值为负， ∴
（注：结合函数
图象同样可以得到），
∴
， ∴
， ∴
.
（Ⅲ）令
，
其中
，则
，
设
， 
∴
在单调递减，
在区间必存在实根，不妨设
即
，可得
（*）
在区间
上单调递增，在
上单调递减， ∴
，
，代入（*）式得
根据题意
恒成立.
又∵
,当且仅当
时,等号成立.
∴
,
，∴
.代入（*）得
,即
.