如图，在△ABC中，AB=AC，D、E是BC边上的点，连接AD、AE，以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E，连接D′C，若BD=CD′﹒
（1）求证：△ABD≌△ACD′；
（2）若∠BAC﹦120°，求∠DAE的度数．
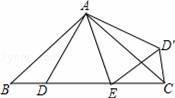
如图，在△ABC中，AB=AC，D、E是BC边上的点，连接AD、AE，以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E，连接D′C，若BD=CD′﹒
（1）求证：△ABD≌△ACD′；
（2）若∠BAC﹦120°，求∠DAE的度数．
【考点】全等三角形的判定与性质；等腰三角形的性质；轴对称的性质．
【分析】（1）根据对称得出AD=AD′，根据SSS证△ABD≌△ACD′即可；
（2）根据全等得出∠BAD=∠CAD′，求出∠BAC=∠DAD′，根据对称得出∠DAE=
∠DAD′，代入求出即可．
【解答】（1）证明：∵以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E，
∴AD=AD′，
∵在△ABD和△ACD′中
，
∴△ABD≌△ACD′；
（2）解：∵△ABD≌△ACD′，
∴∠BAD=∠CAD′，
∴∠BAC=∠DAD′=120°，
∵以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E，
∴∠DAE=∠D′AE=
∠DAD′=60°，
即∠DAE=60°．
【点评】本题考查了全等三角形的性质和判定、对称的性质的应用，主要考查学生的推理能力，题型较好，难度适中．