已知f（x）是定义在R的偶函数，且当x≥0时
．
（1）求f（0）、f（-1）的值；
（2）求f（x）的表达式；
（3）若f（a-1）＜f（3-a），试求a取值范围．
已知f（x）是定义在R的偶函数，且当x≥0时．
（1）求f（0）、f（-1）的值；
（2）求f（x）的表达式；
（3）若f（a-1）＜f（3-a），试求a取值范围．
解：（1）∵当x≥0时，．∴f（0）=0．
f（x）是定义在R的偶函数，f（-1）=f（1），
f（1）=
=-1．
∴f（-1）=-1．
（2）f（x）是定义在R的偶函数，当x＜0时，则-x＞0，
∴f（x）=f（-x）=
故f（x）=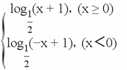
（3）由偶函数的区间对称性的单调性具有相反性，可得：在区间[0，+∞）是减函数，在（-∞，0）是增函数．
由于f（a-1）＜f（3-a），所以：|a-1|＞|3-a|．
解得：a＞2．