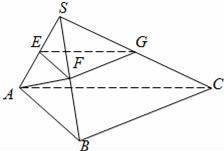
如图,在三棱锥S﹣ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB,过A作AF⊥SB,垂足为F,点E,G分别是棱SA,SC的中点.求证:
(1)平面EFG∥平面ABC;
(2)BC⊥SA.
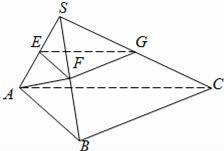
如图,在三棱锥S﹣ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB,过A作AF⊥SB,垂足为F,点E,G分别是棱SA,SC的中点.求证:
(1)平面EFG∥平面ABC;
(2)BC⊥SA.

【考点】直线与平面平行的判定;直线与平面垂直的性质.
【专题】空间位置关系与距离;立体几何.
【分析】(1)根据等腰三角形的“三线合一”,证出F为SB的中点.从而得到△SAB和△SAC中,EF∥AB且EG∥AC,利用线面平行的判定定理,证出EF∥平面ABC且EG∥平面ABC.因为EF、EG是平面EFG内的相交直线,所以平面EFG∥平面ABC;
(2)由面面垂直的性质定理证出AF⊥平面SBC,从而得到AF⊥BC.结合AF、AB是平面SAB内的相交直线且AB⊥BC,可得BC⊥平面SAB,从而证出BC⊥SA.
【解答】解:(1)∵△ASB中,SA=AB且AF⊥SB,∴F为SB的中点.
∵E、G分别为SA、SC的中点,
∴EF、EG分别是△SAB、△SAC的中位线,可得EF∥AB且EG∥AC.
∵EF⊄平面ABC,AB⊂平面ABC,
∴EF∥平面ABC,同理可得EG∥平面ABC
又∵EF、EG是平面EFG内的相交直线,
∴平面EFG∥平面ABC;
(2)∵平面SAB⊥平面SBC,平面SAB∩平面SBC=SB,
AF⊂平面ASB,AF⊥SB.
∴AF⊥平面SBC.
又∵BC⊂平面SBC,∴AF⊥BC.
∵AB⊥BC,AF∩AB=A,∴BC⊥平面SAB.
又∵SA⊂平面SAB,∴BC⊥SA.
【点评】本题在三棱锥中证明面面平行和线线垂直,着重考查了直线与平面平行、平面与平面平行的判定定理,直线与平面垂直的判定与性质等知识,属于中档题.