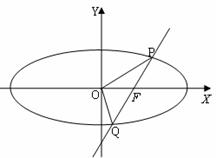
已知直线
过椭圆E:
的右焦点
，且与E相交于
两点.
① 设
（
为原点），求点
的轨迹方程；
② 若直线的倾斜角为
，求
的值.
已知直线过椭圆E:的右焦点，且与E相交于两点.
① 设（为原点），求点的轨迹方程；
② 若直线的倾斜角为，求的值.
解：① 设
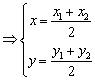
由
，易得右焦点
当直线
轴时，直线
的方程是：
，根据对称性可知
当直线的斜率存在时，可设直线的方程为
代入E有
于是
消去参数
得
而也适上式，故R的轨迹方程是
②设椭圆另一个焦点为
，
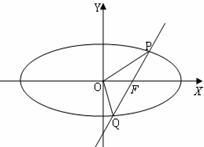
在
中
设
，则
由余弦定理得
.
同理，在
，设
，则
由余弦定理得
.
于是 
.