如图227，求椭圆
＋
＝1的内接矩形中，面积最大的矩形的长和宽及其最大面积.
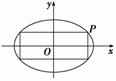
图227
如图227，求椭圆＋＝1的内接矩形中，面积最大的矩形的长和宽及其最大面积.
图227
【解】 已知椭圆＋＝1的参数方程为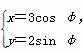
(φ为参数)，
设P(x，y)是椭圆上在第一象限内的一点，
则P点的坐标是P(3cos φ，2sin φ)，
内接矩形面积为
S＝4xy＝4×3cos φ·2sin φ＝12sin 2φ.
当sin 2φ＝1，即φ＝45°时，面积S有最大值12，
这时x＝3cos 45°＝
，y＝2sin 45°＝
.
故面积最大的内接矩形的长为3，宽为2，最大面积为12.