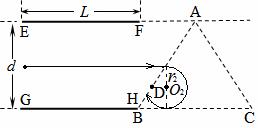
如图所示,板间距为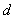 、板长为
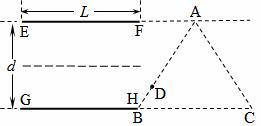
、板长为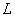 的两块平行金属板EF、GH水平放置,在紧靠平行板右侧的正三角形区域内存在着垂直纸面的匀强磁场,三角形底边BC与GH在同一水平线上,顶点A与EF在同一水平线上。一个质量为
的两块平行金属板EF、GH水平放置,在紧靠平行板右侧的正三角形区域内存在着垂直纸面的匀强磁场,三角形底边BC与GH在同一水平线上,顶点A与EF在同一水平线上。一个质量为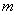 、电量为
、电量为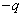 的粒子沿两板中心线以初速度
的粒子沿两板中心线以初速度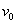 水平射入,若在两板之间加某一恒定电压,粒子离开电场后垂直AB边从D点进入磁场,
水平射入,若在两板之间加某一恒定电压,粒子离开电场后垂直AB边从D点进入磁场,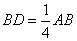 ,并垂直AC边射出(不计粒子的重力),求:
,并垂直AC边射出(不计粒子的重力),求:
(1)两极板间场强的方向
(2)粒子离开电场时瞬时速度的大小;
(3)两极板间电压的大小;
(4)三角形区域内磁感应强度;
(5)若两板间不加电压,三角形区域内的磁场方向垂直纸面向里,要使粒子进入磁场区域后能从AB边射出,试求所加磁场的磁感应强度最小值。
【标准解答】(1)由粒子带负电并且在电场中向下偏转可知,板间场强的方向垂直平行板向下…………………………………………………………………………………①(2分)
(2)垂直AB边进入磁场,由几何知识得:粒子离开电场时偏转角为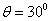
则粒子离开电场时瞬时速度的大小为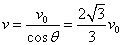 …………………②(1分)
…………………②(1分)
(3)在电场中竖直方向: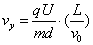 ……………………………………③(2分)
……………………………………③(2分)
由几何关系得,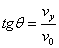 ………………………………………………………④(1分)
………………………………………………………④(1分)
故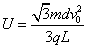 …………………………………………………………………⑤(2分)
…………………………………………………………………⑤(2分)
(4)由几何关系得: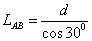 …………………………………………⑥(1分)
…………………………………………⑥(1分)
设在磁场中运动半径为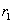 ,则
,则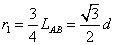 ……………………………⑦(1分)
……………………………⑦(1分)
又 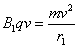 …………………………………………………………………⑧(1分)
…………………………………………………………………⑧(1分)
而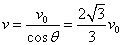 …………………………………………………………⑨(1分)
…………………………………………………………⑨(1分)
以上式子联立得,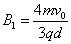 …………………………………………………⑩(2分)
…………………………………………………⑩(2分)
方向:直纸面向外…………………………………………………………………(1分)
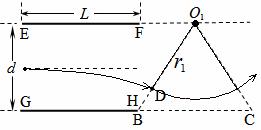
(5)当粒子刚好与BC边相切时,磁感应强度最小,设粒子的运动半径为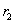 ,
,
由几何知识知: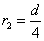 …………………………………………………………⑾(1分 )
…………………………………………………………⑾(1分 )
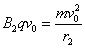 ……………………………………………………………………⑿(1分)
……………………………………………………………………⑿(1分)
故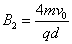 ,即磁感应强度的最小值为………………………………………⒀(1分)
,即磁感应强度的最小值为………………………………………⒀(1分)
【思维点拔】三种场的性质特点:
| | 电场 | 磁场 | 重力场 |
| 力的大小 | ①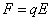 ; ; ②与电荷的运动状态无关,在匀强电场中,电场力为恒力。 | 与电荷的运动状态有关, ①电荷静止或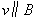 时,不受 时,不受 ; ; ② 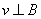 时洛仑兹力最大 时洛仑兹力最大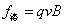 | ①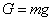 ; ; ②与电荷的运动状态无关 |
| 力的方向 | 正电荷受力方向与 方向相同,(负电荷受力方向与 方向相同,(负电荷受力方向与 相反)。 相反)。 |  方向⊥( 方向⊥(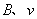 )所决定的平面,(可用左手定则判定) )所决定的平面,(可用左手定则判定)
| 总是竖直向下 |
| 做功特点 | 做功多少与路径无关,只取决于始末两点的电势差,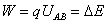 | 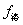 对电荷永不做功,只改变电荷的速度方向,不改变速度的大小 对电荷永不做功,只改变电荷的速度方向,不改变速度的大小
| 做功多少与路径无关,只取决于始末位置的高度差,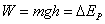 |
![]() 、板长为
、板长为![]() 的两块平行金属板EF、GH水平放置,在紧靠平行板右侧的正三角形区域内存在着垂直纸面的匀强磁场,三角形底边BC与GH在同一水平线上,顶点A与EF在同一水平线上。一个质量为
的两块平行金属板EF、GH水平放置,在紧靠平行板右侧的正三角形区域内存在着垂直纸面的匀强磁场,三角形底边BC与GH在同一水平线上,顶点A与EF在同一水平线上。一个质量为![]() 、电量为
、电量为![]() 的粒子沿两板中心线以初速度
的粒子沿两板中心线以初速度![]() 水平射入,若在两板之间加某一恒定电压,粒子离开电场后垂直AB边从D点进入磁场,
水平射入,若在两板之间加某一恒定电压,粒子离开电场后垂直AB边从D点进入磁场,![]() ,并垂直AC边射出(不计粒子的重力),求:
,并垂直AC边射出(不计粒子的重力),求:


