椭圆G：的两个焦点F1（－c，0）、F2（c，0），M是椭圆上的一点，且

椭圆G：的两个焦点F₁（－c，0）、F₂（c，0），M是椭圆上的一点，且满足

  （Ⅰ）求离心率e的取值范围；

 （Ⅱ）当离心率e取得最小值时，点N（0，3）到椭圆上的点的最远距离为求此时椭圆G的方程；（ⅱ）设斜率为k（k≠0）的直线l与椭圆G相交于不同的两点A、B，Q为AB的中点，问A、B两点能否关于过点的直线对称？若能，求出k的取值范围；若不能，请说明理由

（1）；（2）(i)所求椭圆方程为，（ⅱ）当时，A、B两点关于点P、Q的直线对称。

（I）设M（x₀，y₀）

                 ①

又  ②

由②得代入①式整理得

又

解得

（Ⅱ）（i）当

设H（x，y）为椭圆上一点，则

若0

由（舍去）

若b≥3，当y=－3时，|HN|²有最大值2b²+18

由2b²+18=50得b²=16

∴所求椭圆方程为

（ii）设A（x₁，y₁），B（x₂，y₂），Q（x₀，y₀），则由

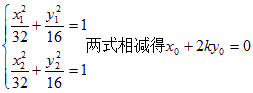             ③

又直线PQ⊥直线l    ∴直线PQ方程为

将点Q（x₀，y₀）代入上式得，    ④

由③④得Q

（解1）而Q点必在椭圆内部   

由此得

故当时A、B两点关于点P、Q的直线对称

（解2）∴AB所在直线方程为

由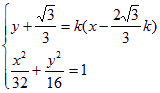得

显然1+2k²≠0

而

直线l与椭圆有两不同的交点A、B  ∴△＞0

解得

故当时，A、B两点关于点P、Q的直线对称。

（ii）另解；设直线l的方程为y=kx+b

由得

设A（x₁，y₁），B（x₂，y₂），Q（x₀，y₀），则

      ③

又直线PQ⊥直线l    ∴直线PQ方程为

将点Q（x₀，y₀）代入上式得，    ④

将③代入④⑤

∵x₁，x₂是（*）的两根

⑥

⑤代入⑥得

∴当时，A、B两点关于点P、Q的直线对称。