已知数列
中，
，
，
.
（1）求证：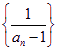
是等差数列；并求数列的通项公式；
（2）假设对于任意的正整数
、
，都有
，则称该数列为“
域收敛数列”. 试判断: 数列
，是否为一个“
域收敛数列”，请说明你的理由.
已知数列中，，，.
（1）求证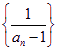：是等差数列；并求数列的通项公式；
（2）假设对于任意的正整数、，都有，则称该数列为“域收敛数列”. 试判断: 数列，是否为一个“域收敛数列”，请说明你的理由.
（1）证明略 
（2）是
（1）证明：因为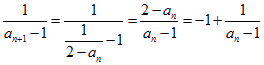
，
所以
，
；故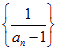
是等差数列.
由此可得，
，
所以
，.
（2）解：由条件
，可知
当
，
；当
时，
，
.
令
，则
所以，当
时，
；
同理可得，当
时，
；
即数列
在
时递增；
时，递减；即
是数列的最大项.
然而，因为
的奇数项均为
，故
为数列的最小项；
而
，
，所以
，
故
是数列的最大项.
因此，对任意的正整数
、
，
所以数列，是一个“
域收敛数列”.