(本小题满分14分)已知点![]() 的坐标分别是
的坐标分别是![]() ,
,![]() ,直线
,直线![]() 相交于点M,且它们的斜率之积为
相交于点M,且它们的斜率之积为![]() .(1)求点M轨迹
.(1)求点M轨迹![]() 的方程;(2)若过点
的方程;(2)若过点![]() 的直线
的直线![]() 与(1)中的轨迹
与(1)中的轨迹![]() 交于不同的两点
交于不同的两点![]() 、
、![]() (
(![]() 在
在![]() 、
、![]() 之间),试求
之间),试求![]() 与
与![]() 面积之比的取值范围(
面积之比的取值范围(![]() 为坐标原点).
为坐标原点).
(本小题满分14分)已知点![]() 的坐标分别是
的坐标分别是![]() ,
,![]() ,直线
,直线![]() 相交于点M,且它们的斜率之积为
相交于点M,且它们的斜率之积为![]() .(1)求点M轨迹
.(1)求点M轨迹![]() 的方程;(2)若过点
的方程;(2)若过点![]() 的直线
的直线![]() 与(1)中的轨迹
与(1)中的轨迹![]() 交于不同的两点
交于不同的两点![]() 、
、![]() (
(![]() 在
在![]() 、
、![]() 之间),试求
之间),试求![]() 与
与![]() 面积之比的取值范围(
面积之比的取值范围(![]() 为坐标原点).
为坐标原点).
(1)![]() (
(![]() )(2)
)(2)![]()
(1)设点![]() 的坐标为
的坐标为![]() ,∵
,∵![]() ,∴
,∴![]() . 整理,得
. 整理,得
![]() (
(![]() ),这就是动点M的轨迹方程.
),这就是动点M的轨迹方程.
(2)方法一 由题意知直线![]() 的斜率存在,设
的斜率存在,设![]() 的方程为
的方程为![]() (
(![]() ) ①
) ①
将①代入![]() ,得
,得![]() ,由
,由![]() ,解得
,解得![]() .
.
设![]() ,
,![]() ,则
,则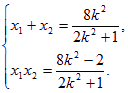 ②
②
令![]() ,则
,则![]() ,即
,即![]() ,即
,即![]() ,且
,且![]()
由②得,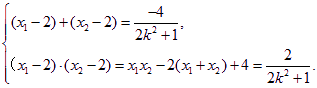
即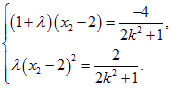
![]() .
.
![]() 且
且![]()
![]() 且
且![]() .
.
解得![]() 且
且![]()
![]() ,
,![]() 且
且![]() .
.
∴△OBE与△OBF面积之比的取值范围是![]() .
.
方法二 由题意知直线![]() 的斜率存在,设
的斜率存在,设![]() 的方程为
的方程为![]()
![]() ①
①
将①代入![]() ,整理,得
,整理,得![]() , 由
, 由![]() ,解得
,解得![]() .
.
设![]() ,
,![]() ,则
,则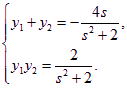 ②
②
令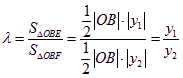 ,且
,且![]() .将
.将![]() 代入②,得
代入②,得
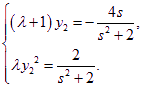 ∴
∴![]() .即
.即![]() .
.
∵![]() 且
且![]() ,∴
,∴![]() 且
且![]() .即
.即![]() 且
且![]() .解得
.解得
![]() 且
且![]() .
. ![]() ,
,![]() 且
且![]() .
.
故△OBE与△OBF面积之比的取值范围是![]() .
.