（1）求a的值；
（2）对于某项am，存在bn，使am+1=bn成立，求b的值并推导m与n的关系式；
（3）在｛an｝中，对于满足（2）的项，求它的前k项和.
（1）求a的值；
（2）对于某项am，存在bn，使am+1=bn成立，求b的值并推导m与n的关系式；
（3）在｛an｝中，对于满足（2）的项，求它的前k项和.
解：（1）∵a1＜b1＜a2＜b2＜a3，
∴
∴
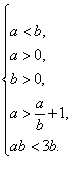
∴a=2（b＞a=2）.
（2）由am+1=bn，得a+b（m-1）+1=b·2n-1，
∴3+b（m-1）=b·2n-1.
∴
+m-1=2n-1.
∴
∈N.又∵b＞2，∴b=3，m=2n-1.
（3）由（2）知，am=bn-1=3·2n-1-1，
所以｛an｝中满足（2）的项的前k项和Sk=（3×21-1-1）+（3×22-1-1）+（3×23-1-1）+…+（3×2k-1-1）=3-1+3×2-1+3×22-1+…+3×2k-1-1=3-k+3×（2+22+…+2k-1）=3-k+3×
=3·2k-k-3.