首页 / 若椭圆=1（m＞n＞0）和双曲线=1（a＞b＞0）有相同的左、右焦点F1、F2

若椭圆=1（m＞n＞0）和双曲线=1（a＞b＞0）有相同的左、右焦点F1、F2

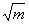
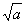
若椭圆=1（m＞n＞0）和双曲线=1（a＞b＞0）有相同的左、右焦点F1、F2，P是两条曲线的一个交点，则|PF1|·|PF2|的值是（　　）

A.m-a

B.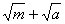（m-a）

C.m2-a2

D.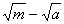

答案

解析：

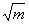
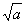
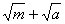
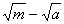
不妨设点P在第一象限，由已知|PF1|+|PF2|=2,|PF1|-|PF2|=2,则|PF1|=,|PF2|=,故|PF1|·|PF2|=m-a,选A.

答案：

A

相关题目

动物细胞的有丝分裂过程与植物细胞明显不同的是   （  ）
动物细胞的有丝分裂过程与植物细胞明显不同的是   （  ）                 A．间期有染色体的复制                 B．后期有着丝点
读长江河道入海示意图，回答下列问题。 (1)河港的选择需要
读长江河道入海示意图，回答下列问题。 (1)河港的选择需要一定的水深，某港务局拟在A、B两处建港，应当选择在 处，理由是。 (2)某勘探队在C处钻探
合成橡胶的原料和单体分别是( ) A．石油、天然气；二烯烃
合成橡胶的原料和单体分别是( ) A．石油、天然气；二烯烃、烯烃 B．沼气；烯烃 C．裂化气；乙烯 D．焦炉气；甲烷
名篇名句填空（从5小题中选择3题作答） ⑴青山隔送行，  
名篇名句填空（从5小题中选择3题作答） ⑴青山隔送行，                       ，                        。夕阳古道无人语，禾
已知双曲线 (a＞0，b＞0)的一条渐近线过点，且双曲线的一个
已知双曲线 (a＞0，b＞0)的一条渐近线过点，且双曲线的一个焦点为，则双曲线的方程为      ．
已知集合满足： 且 则“”是“”的(    ) A．充要条件   
已知集合满足： 且 则“”是“”的(    ) A．充要条件                                                  B．充分不必要条件 C
下列对物质性质的归纳中，正确的是  (      )A．H2、O2、C
下列对物质性质的归纳中，正确的是  (      )A．H2、O2、CH4都具有可燃性             B．H2、C、CO都能和CuO发生置换反应C．浓硫酸、浓盐酸、
(2008年上海卷)核糖与核酸都不含有的元素是( ) A．N       
(2008年上海卷)核糖与核酸都不含有的元素是( ) A．N                                B．O C．P                              

最新题目

阅读《倔强的仙人掌》 倔强的仙人掌 ①女人看见路边蹲
若，，则代数式          ，代数式 =         ．
创刊于1861年的《上海新报》称：“因上海地方五方杂处，各
根据以下材料，自取角度，自拟题目，写一篇不少于800字的
如图所示，质量m＝2 kg的小球用长L＝1.05 m的轻质细绳悬挂在
阅读《斑羚飞渡》，回答文后的问题。试跳成功。紧接着，
某无色溶液中加入过量盐酸有沉淀产生，过滤后向滤液中加
固定斜面C的倾角为，物体A放在斜面C上，物体B叠放在物体A上
 Both my parents were born ____    1970. A. at  B. in C. on D. to
有人评论说：“本诗一咏三叹的写法是对《诗经》中复沓形
材料一：1995年5月6日颁布的《中共中央、国务院关于加速科
世界上现存最早标有确切日期的雕版印刷品是（ ） A．《金
 – I’m afraid I can’t go to the party tomorrow.    – _______ you tol
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，给下以下结
下列选项中不属于人体防线的是                   
18．阅读材料，回答问题。 材料一：第十五届世界气候变化
不等式对恒成立，则的取值范围是（    ） A.   B.   C.   
在果实的成熟过程中，起主要作用的激素是 A．乙烯      
阅读下文，完成文后各题。 我个人认为，中华文化虽然博大
某班举行辩论会，下图所示为双方辩手的主要观点。据此判