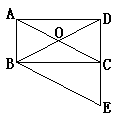
如图,![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点.
的中点.
操作:过点![]() 做
做![]() 的垂线,过点
的垂线,过点![]() 作
作![]() 的平行线,两直线相交于点
的平行线,两直线相交于点![]() ,在
,在![]() 的延长线上截取
的延长线上截取![]() ,联结
,联结![]() 、
、![]() .
.
(1)试判断![]() 与
与![]() 之间有怎样的关系,并证明你所得的结论;
之间有怎样的关系,并证明你所得的结论;
(2)如果![]() ,
,![]() ,求
,求![]() 的长.
的长.
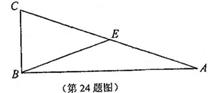
如图,![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点.
的中点.
操作:过点![]() 做
做![]() 的垂线,过点
的垂线,过点![]() 作
作![]() 的平行线,两直线相交于点
的平行线,两直线相交于点![]() ,在
,在![]() 的延长线上截取
的延长线上截取![]() ,联结
,联结![]() 、
、![]() .
.
(1)试判断![]() 与
与![]() 之间有怎样的关系,并证明你所得的结论;
之间有怎样的关系,并证明你所得的结论;
(2)如果![]() ,
,![]() ,求
,求![]() 的长.
的长.

解:(1)如图①,过点G作![]() 于M.
于M.
在正方形EFGH中,
![]() . ………………………1分
. ………………………1分
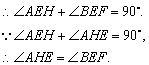
又∵![]() ,
,
∴⊿AHE≌⊿BEF. ………………………2分
同理可证:⊿MFG≌⊿BEF. ………………………3分
∴GM=BF=AE=2.
∴FC=BC-BF=10. ………………………4分
(2)如图②,过点G作![]() 于M.连接HF.
于M.连接HF.
![]()
![]() ………………………5分
………………………5分
又![]()
∴⊿AHE≌⊿MFG. ………………………6分
∴GM=AE=2. ………………………7分
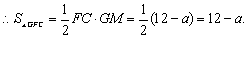 ………………………8分
………………………8分
(3)⊿GFC的面积不能等于2. ………………………9分
∵若![]() 则12- a =2,∴a=10.
则12- a =2,∴a=10.
此时,在⊿BEF中,
![]() ……………10分
……………10分
在⊿AHE中,
![]() .…11分
.…11分
∴AH>AD.
即点H已经不在边AB上.
故不可能有![]() ………………………………………12分
………………………………………12分
解法二:⊿GFC的面积不能等于2. ………………………9分
∵点H在AD上,
∴菱形边长EH的最大值为![]() .
.
∴BF的最大值为![]() . ………………………10分
. ………………………10分
又因为函数![]() 的值随着a的增大而减小,
的值随着a的增大而减小,
所以![]() 的最小值为
的最小值为![]() . ………………………11分
. ………………………11分
又∵![]() ,∴⊿GFC的面积不能等于2. ………………12分
,∴⊿GFC的面积不能等于2. ………………12分