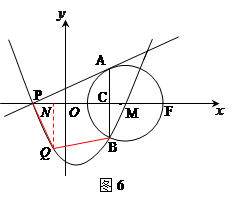
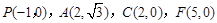两点，过点P（－1，0）作⊙M的切线，切点为点A，过点A作AB⊥x轴于点C，交⊙M于
点B。抛物线y＝ax2＋bx＋c经过P、B、M三点。
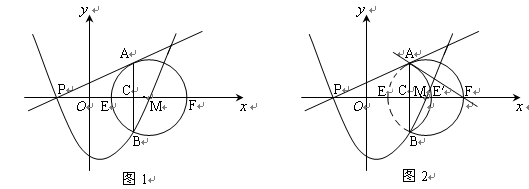
【小题1】（1）求该抛物线的函数表达式；（3分）
【小题2】（2）若点Q是抛物线上一动点，且位于P、B两点之间，设四边形APQB的面积为S，点Q的
横坐标为x，求S与x之间的函数关系式，并求S的最大值和此时点Q的坐标；（4分）
【小题3】（3）如图2，将弧AEB沿弦AB对折后得到弧AE′B，试判断直线AF与弧AE′B的位置关系，
并说明理由。（3分）
点
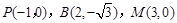
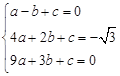
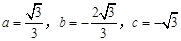
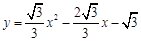
∵点Q是抛物线上一动点，且位于P、B两点之间，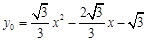
，－1≤x≤2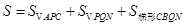 
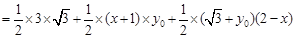
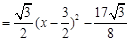；（其中，－1≤x≤2）
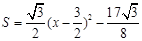；（其中，－1≤x≤2）
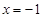时，四边形APQB的面积S有最大值，
,，
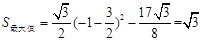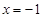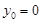，点Q的坐标为（－1，0），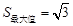
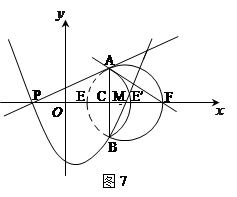（3）直线AF与弧AE′B相切，理由如下：