如图，在△ABC中，∠C=90°，AC=8，BC=6，D是边AB的中点，现有一点P位于边AC上，使得△ADP与△ABC相似，则线段AP的长为 ．
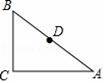
如图，在△ABC中，∠C=90°，AC=8，BC=6，D是边AB的中点，现有一点P位于边AC上，使得△ADP与△ABC相似，则线段AP的长为 ．
4或
．
【考点】相似三角形的判定．
【分析】先根据勾股定理求出AB的长，再分△ADP∽△ABC与△ADP∽△ACB两种情况进行讨论即可．
【解答】解：∵在△ABC中，∠C=90°，AC=8，BC=6，
∴AB=
=10．
∵D是边AB的中点，
∴AD=5．
当△ADP∽△ABC时，
=
，即
=
，解得AP=4；
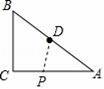
当△ADP∽△ACB时，
=
，即
=
，解得AP=．
故答案为：4或．
【点评】本题考查的是相似三角形的判定，在解答此题时要注意进行分类讨论，不要漏解．