(09年莱阳一中期末理)(12分)四棱锥![]() 中,
中,
![]() ,E为PA中点,过E作平行于底面的面EFGH分别与另外三条侧棱交于F, G,H已知底面ABCD为直角梯形,AD∥BC,
,E为PA中点,过E作平行于底面的面EFGH分别与另外三条侧棱交于F, G,H已知底面ABCD为直角梯形,AD∥BC,![]() ,
,![]() 。
。
(1)求异面直线AF,BG所成的角的大小;
(2)设面APB与面CPD所成的锐二面角的大小为![]() ,求cos
,求cos![]() .
.
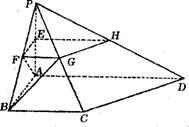
(09年莱阳一中期末理)(12分)四棱锥![]() 中,
中,
![]() ,E为PA中点,过E作平行于底面的面EFGH分别与另外三条侧棱交于F, G,H已知底面ABCD为直角梯形,AD∥BC,
,E为PA中点,过E作平行于底面的面EFGH分别与另外三条侧棱交于F, G,H已知底面ABCD为直角梯形,AD∥BC,![]() ,
,![]() 。
。
(1)求异面直线AF,BG所成的角的大小;
(2)设面APB与面CPD所成的锐二面角的大小为![]() ,求cos
,求cos![]() .
.

解析:由题意可知,AP、AD、AB两两垂直,可建立空间直角坐标系A-![]() ,
,
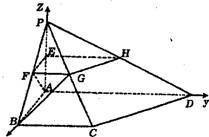
由平面几何知识知:AD=4,D(0,4,0),B(2,0,0),C(2,2,0),P(0,0,2),E(0,0,1),F(1,0,1),G(1,1,1)…………2分
(1)![]() ,
,![]() ,
,
∴![]() =0
=0
∴AF与BG所成的角为![]() ……………………4分
……………………4分
(2)可证明AD![]() 平面APB,∴平面APB的法向量为
平面APB,∴平面APB的法向量为![]()
设平面CPD的法向量为![]() ,由
,由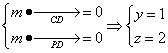
∴![]() ……………………………………………………………………10分
……………………………………………………………………10分
∴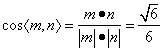 ,即
,即![]() ………………………………12分
………………………………12分