.如图,正方形ABCD与正三角形AEF的顶点A重合,将△AEF绕其顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小可以是 .
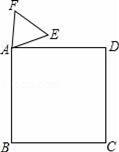

.如图,正方形ABCD与正三角形AEF的顶点A重合,将△AEF绕其顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小可以是 .


15°或165° .
【考点】旋转的性质;等边三角形的性质;正方形的性质.
【分析】利用正方形的性质和等边三角形的性质证明△ABE≌△ADF(SSS),有相似三角形的性质和已知条件即可求出当BE=DF时,∠BAE的大小,应该注意的是,正三角形AEF可以在正方形的内部也可以在正方形的外部,所以要分两种情况分别求解.
【解答】解:①当正三角形AEF在正方形ABCD的内部时,如图1,
∵正方形ABCD与正三角形AEF的顶点A重合,
当BE=DF时,
在△ABE与△ADF中,

 ,
,
∴△ABE≌△ADF(SSS),
∴∠BAE=∠FAD,
∵∠EAF=60°,
∴∠BAE+∠FAD=30°,
∴∠BAE=∠FAD=15°,
②当正三角形AEF在正方形ABCD的外部时.
∵正方形ABCD与正三角形AEF的顶点A重合,
当BE=DF时,
∴AB=AD BE=DF AE=AF,
∴△ABE≌△ADF(SSS),
∴∠BAE=∠FAD,
∵∠EAF=60°,
∴∠BAE=(360°﹣90°﹣60°)×![]()
![]() +60°=165°,
+60°=165°,
∴∠BAE=∠FAD=165°
故答案为:15°或165°.




【点评】本题考查了正方形的性质、等边三角形的性质、旋转的性质以及全等三角形的判定和全等三角形的性质和分类讨论的数学思想,题目的综合性不小.