已知x∈[0，1]，函数f（x）=x2﹣ln（x+
），g（x）=x3﹣3a2x﹣4a．
（1）求函数f（x）的单调区间和值域；
（2）设a≤﹣1，若∀x1∈[0，1]，总存在x0∈[0，1]，使得g（x0）=f（x1）成立，求a的取值范围．
已知x∈[0，1]，函数f（x）=x2﹣ln（x+），g（x）=x3﹣3a2x﹣4a．
（1）求函数f（x）的单调区间和值域；
（2）设a≤﹣1，若∀x1∈[0，1]，总存在x0∈[0，1]，使得g（x0）=f（x1）成立，求a的取值范围．
【考点】利用导数求闭区间上函数的最值；利用导数研究函数的单调性．
【专题】计算题；函数的性质及应用；导数的综合应用．
【分析】（1）求导数f′（x）=2x﹣
=
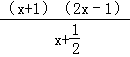；从而由导数的正负确定函数的单调区间及值域；
（2）设g（x）在[0，1]上的值域为[b，c]，则有b≤
且c≥ln2；再求导g′（x）=3x2﹣3a2，从而确定函数的单调性，从而化为最值问题．
【解答】解：（1）f′（x）=2x﹣=；
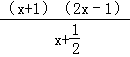令f′（x）＜0解得，0≤x＜；
故函数f（x）的单调减区间为[0，]，
此时，≤f（x）≤ln2；
令f′（x）＞0解得，＜x≤1；
故函数f（x）的单调增区间[，1]，
此时，≤f（x）≤ln3﹣ln2；
故函数f（x）的值域为[，ln2]．
（2）根据所给条件，设g（x）在[0，1]上的值域为[b，c]，
则有b≤且c≥ln2；
g′（x）=3x2﹣3a2＜0，
g（x）在[0，1]上是单调减函数，
故g（0）=﹣4a≥ln2，
解得a≤﹣
；
g（1）=1﹣3a2﹣4a≤，
解得a≤﹣
或a≥
；
故a≤﹣．
【点评】本题考查了导数的综合应用及函数的性质应用，同时考查了恒成立问题，属于中档题．