已知P是圆M：x2+y2+4x+4-4m2=0(m>0且m≠2)上任意一点，点N的坐标为(2，0)，线段NP的垂直平分线交直线MP于点Q，当点P在圆M上运动时，点Q的轨迹为C。
（1）求出轨迹C的方程，并讨论曲线C的形状；
（2）当m=
时，在x轴上是否存在一定点E，使得对曲线C的任意一条过E的弦AB，
为定值？若存在，求出定点和定值；若不存在，请说明理由。
已知P是圆M：x2+y2+4x+4-4m2=0(m>0且m≠2)上任意一点，点N的坐标为(2，0)，线段NP的垂直平分线交直线MP于点Q，当点P在圆M上运动时，点Q的轨迹为C。
（1）求出轨迹C的方程，并讨论曲线C的形状；
（2）当m=时，在x轴上是否存在一定点E，使得对曲线C的任意一条过E的弦AB，为定值？若存在，求出定点和定值；若不存在，请说明理由。
（1）m>2，
，以N，P为焦点的椭圆
M<2，
，以N，P为焦点的双曲线
（2）由（1）曲线C为
，
设
，分别过E取两垂直于坐标轴的两条弦CD，
，
则
，即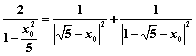
解得
，∴E若存在必为
定值为6.
下证满足题意。
设过点E
的直线方程为
，代入C中得:
，设
、
，
则
，
.
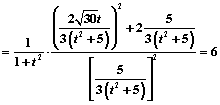同理可得E
也满足题意。
综上得定点为E，定值为