（１３分）2011年7月23日上海铁路局管辖内的杭深线动车组因列车追

（１３分）2011年7月23日上海铁路局管辖内的杭深线动车组因列车追尾而发生大量人员伤亡的惨烈事故。现有A、B两列火车,在同一轨道上同向行驶，A车在前，其速度v_A=10 m/s，B车速度v_B=30 m/s。因大雾能见度很低，B车在距A车600 m时才发现前方有A车，这时B车立即刹车，但B车要经过1800 m才能够停止。问：

(1) A车若按原速前进，两车是否会相撞？若会相撞,将在何时何地？

(2) 若B车司机在刹车后发出信号，A车司机接收到信号后以加速度a₁=0.25m/s²加速前进，已经比B车刹车时刻晚了Δt=8s, 问是否能避免事故？若能够避免，求两车的最小距离。

解：(1)以A车为参考系，设在B车恰能追上A车的情况下，A、B两车之间的初始间距为s₀，则

(v_B－v_A)²=2as₀                                                       ①                    2分

再以地面为参考系，设B车的最大滑行距离为s₁，则

v_B²=2as₁                                                        ②                          1分

解①②两式可得s₀=800 m

因为s₀＞600 m，所以两车一定相撞。设两车经时间t相撞，则有：

vt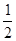－at₂=v_At+s                                                 ③                      2分

由②式得：a=0.25 m/s²,代入③式得t=40 s（t=120s舍去）            2分

设相撞地点距B车刹车地点s_B，则有s_B=v_At+s =1000 m.                 2分

(2)设B车减速t1秒时两车的速度相同：

      v_B -at₁=v_A +a₁(t₁-Δt)                

代入数解得t₁=44s                                                2分

在此过程中：     S_B = v_Bt₁-at₁²/2 =1078 m

S_A= v_A t₁+a₁(t₁-Δt)²/2=602m

S_A +S＞S_B 不会发生撞车事故。

此时ΔS= S_A +S- S_B =124m                                          2分

 解析:略