设函数
（
为常数），且
在
上单调递减。
（1）求实数的取值范围；
（2）当取得最大值时，关于
的方程
有3个不同的根，求实数
的取值范围。
设函数（为常数），且在上单调递减。
（1）求实数的取值范围；
（2）当取得最大值时，关于的方程有3个不同的根，求实数
的取值范围。
解：（1）依题意得：
在
上单调递减 
在恒成立
即：当
时，
当
时，
在
恒成立
记
则
只须
综上，·························································（４分）
（2）当
时，方程
有3个不同根等价
有3个不同根
记
则
令
得
或
令
得
在
递增，在
递减
要使有3个不同根
只须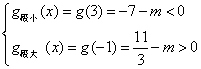
…………11分
得
······················································（８分）