=1,抛物线C2：(y-m)2=2px(p＞0),且C1、C2的公共弦AB过椭圆C1的右焦点.(1)当AB⊥x轴时，求m、p的值，并判断抛物线C2的焦点是否在直线AB上；
(2)若p=
且抛物线C2的焦点在直线AB上，求m的值及直线AB的方程.
=1,抛物线C2：(y-m)2=2px(p＞0),且C1、C2的公共弦AB过椭圆C1的右焦点.(1)当AB⊥x轴时，求m、p的值，并判断抛物线C2的焦点是否在直线AB上；
(2)若p=且抛物线C2的焦点在直线AB上，求m的值及直线AB的方程.
解：
（1）当AB⊥x轴时，点A、B关于x轴对称.所以m=0，直线AB的方程为x=1，从而点A的坐标为（1，
）.因为点A在抛物线上，所以
.此时C2的焦点坐标为（
（2）当C2的焦点在AB上时，由（1）知直线AB的斜率存在，设直线AB的方程为y=k(x-1).
由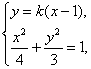
消去y得（3+4k2）x2-8k2x+4k2-12=0 ①
设A、B的坐标分别为（x1,y1）(x2,y2),
则x1、x2是方程①的两根，x1+x2=
因为AB既是过C1的右焦点的弦，又是过C2的焦点的弦，
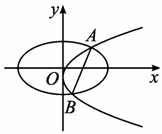
所以|AB|=（2-
x2)=4-
(x1+x2),且|AB|=（x1+
)=x1+x2+p=x1+x2+
.从而x1+x2+
(x1+x2).所以x1+x2=
解得k2=6,即k=±
因为C2的焦点F′(
所以m=-
或m=-
.当m=
(x-1);当m=-
(x-1).