(1)求导体棒ab从A下落r/2时的加速度大小。
(2)若导体棒ab进入磁场II后棒中电流大小始终不变,求磁场I和II之间的距离h和R2上的电功率P2。
(3)当导体棒进入磁场II时,施加一竖直向上的恒定外力F=mg的作用,求导体棒ab从开始进入磁场II到停止运动所通过的距离和电阻R2上所产生的热量。
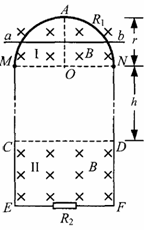
(1)求导体棒ab从A下落r/2时的加速度大小。
(2)若导体棒ab进入磁场II后棒中电流大小始终不变,求磁场I和II之间的距离h和R2上的电功率P2。
(3)当导体棒进入磁场II时,施加一竖直向上的恒定外力F=mg的作用,求导体棒ab从开始进入磁场II到停止运动所通过的距离和电阻R2上所产生的热量。

解:(1)(6分)以导体棒为研究对象,棒在磁场I中切割磁感线,棒中产生产生感应电动势,导体棒ab从A下落r/2时,导体棒在重力与安培力作用下做加速运动,
由牛顿第二定律,得![]() ①(1分)
①(1分)
式中![]() ②(1分)
②(1分)
![]() ③(1分)
③(1分)
![]() =4R ④(2分)
=4R ④(2分)
由以上各式可得到 ![]() ⑤(1分)
⑤(1分)
(2)(8分)当导体棒ab通过磁场II时,若安培力恰好等于重力,棒中电流大小始终不变,即![]() , ⑥(1分)
, ⑥(1分)
![]() ⑦(1分)
⑦(1分)
(或![]() )
)
式中![]() ⑧(1分)
⑧(1分)
解得 ![]() ⑨(2分)
⑨(2分)
导体棒从MN到CD做加速度为g的匀加速直线运动,有
![]() ⑩ (1分)
⑩ (1分)
得 ![]()
![]() (2分)
(2分)
(3)(6分)由动量定理得 ![]()
![]() (1分)
(1分)
即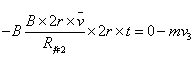
![]()
![]()
即![]()
![]() (1分)
(1分)
联立⑨![]() 解得
解得![]()
![]() (1分)
(1分)
停下来过程中重力做正功、外力F和安培力做负功,由动能定理有
![]()
所以产生总热量为
![]()
![]() (1分)
(1分)
在电阻R2上产生的热量为![]()
![]() (1分)
(1分)
联立⑨![]()
![]() 解得:
解得:![]() (1分)
(1分)