(本题满分18分)第一题满分4分,第二题满分6分,第三题满分8分.
已知椭圆![]() 的长轴长是焦距的两倍,其左、右焦点依次为
的长轴长是焦距的两倍,其左、右焦点依次为![]() 、
、![]() ,抛物线
,抛物线![]()
![]() 的准线与
的准线与![]() 轴交于
轴交于![]() ,椭圆
,椭圆![]() 与抛物线
与抛物线![]() 的一个交点为
的一个交点为![]() .
.
(1)当![]() 时,求椭圆
时,求椭圆![]() 的方程;
的方程;
(2)在(1)的条件下,直线![]() 过焦点
过焦点![]() ,与抛物线
,与抛物线![]() 交于
交于![]() 两点,若弦长
两点,若弦长![]() 等于
等于![]() 的周长,求直线
的周长,求直线![]() 的方程;
的方程;
(3)由抛物线弧![]()
![]() 和椭圆弧
和椭圆弧![]()
![]()
(![]() )合成的曲线叫“抛椭圆”,是否存在以原点
)合成的曲线叫“抛椭圆”,是否存在以原点![]() 为直角顶点,另两个顶点
为直角顶点,另两个顶点![]() 落在“抛椭圆”上的等腰直角三角形
落在“抛椭圆”上的等腰直角三角形![]() ,若存在,求出两直角边所在直线的斜率;若不存在,说明理由.
,若存在,求出两直角边所在直线的斜率;若不存在,说明理由.

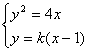 得,
得,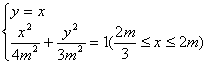 得
得