（本题满分18分，第（1）小题4分，第2小题6分，第3小题8分）
已知点，
，…，
（
为正整数）都在函数
的图像上，其中
是以1为首项，2为公差的等差数列。
（1）求数列的通项公式，并证明数列
是等比数列；
（2）设数列的前项的和
，求
；
（3）设
，当
时，问
的面积是否存在最大值？若存在，求出最大值；若不存在，请说明理由；
（本题满分18分，第（1）小题4分，第2小题6分，第3小题8分）
已知点，，…，（为正整数）都在函数的图像上，其中是以1为首项，2为公差的等差数列。
（1）求数列的通项公式，并证明数列是等比数列；
（2）设数列的前项的和，求；
（3）设，当时，问的面积是否存在最大值？若存在，求出最大值；若不存在，请说明理由；
（本题满分18分，第（1）小题4分，第2小题6分，第3小题8分）
解：（1）
，（
，
2分
，
，
是等比数列。
………………………. 4分
(2)因为
是等比数列，且公比
，
，
。
…………………………………………………. 6分
当
时，
；
…………………………………………………. 7分
当
时，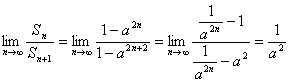
。
…………………………………………………. 9分
因此，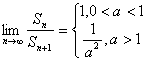
。
…………………………………………………. 10分
（3）
，
，
………………………………………………….12分
设
，当
最大时，则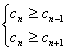
，
…………………………………………………. 14分
解得
，
，
。
…………………………………………………. 16分
所以
时取得最大值
，因此
的面积存在最大值。
…………………………………………………. 18分