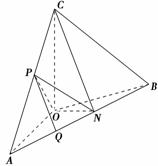
如图，在四面体ABOC中，OC⊥OA，OC⊥OB，∠AOB＝120°，且OA＝OB＝OC＝1. (

如图，在四面体ABOC中，OC⊥OA，OC⊥OB，∠AOB＝120°，且OA＝OB＝OC＝1.

(1)设P为AC的中点．证明：在AB上存在一点Q，使PQ⊥OA，并计算的值；

(2)求二面角O－AC－B的平面角的余弦值．

解法一：(1)在平面OAB内作ON⊥OA交AB于N，连结NC.

又OA⊥OC，∴OA⊥平面ONC.∵NC⊂平面ONC，∴OA⊥NC.取Q为AN的中点，则PQ∥NC，

∴PQ⊥OA.在等腰△AOB中，∠AOB＝120°，∴∠OAB＝∠OBA＝30°.在Rt△AON中，∠OAN

＝30°，∴ON＝AN＝AQ.在△ONB中，∠NOB＝120°－90°＝30°＝∠NBO，∴NB＝ON＝AQ，∴＝3.

(2)连结PN，PO.由OC⊥OA，OC⊥OB知OC⊥平面OAB.又ON⊂平面OAB，∴OC⊥ON.

又由ON⊥OA知ON⊥平面AOC.∴OP是NP在平面AOC内的射影．

在等腰Rt△COA中，P为AC的中点，∴AC⊥OP.

根据三垂线定理，知AC⊥NP.∴∠OPN为二面角O－AC－B的平面角．在等腰Rt△COA中，OC＝OA＝1，∴OP＝.在Rt△AON中，ON＝OAtan 30°＝，

∴在Rt△PON中，PN＝＝，∴cos ∠OPN＝＝＝.

解法二：(1)取O为坐标原点，分别以OA，OC所在的直线为x轴，z轴，建立空间直角坐标系O－xyz(如图所示)

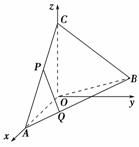
则A(1,0,0)，C(0,0,1)，B.∵P为AC中点，∴P.

设＝λ(λ∈(0,1))，∵＝，

∴＝＋＝(1,0,0)＋λ＝，

∴＝－＝.

∵PQ⊥OA，∴·＝0，即－λ＝0，λ＝.所以存在点Q使得PQ⊥

OA且＝3.

（2）记平面ABC的法向量为n=（n₁，n₂，n₃），则由n⊥，n⊥，且＝(1,0，－1)，

得故可取n＝(1，，1)．

又平面OAC的法向量为e＝(0,1,0)．

∴cos〈n，e〉＝＝.

二面角O－AC－B的平面角是锐角，记为θ，则cos θ＝.