已知
是定义在
上的奇函数，且
，若
时，有
.
(1)求证：在上为增函数；
(2)求不等式
的解集；
(3)若
对所有
恒成立，求实数
的取值范围.
已知是定义在上的奇函数，且，若 时，有.
(1)求证：在上为增函数；
(2)求不等式的解集；
(3)若对所有恒成立，求实数的取值范围.
解：（1）证明：任取
且
，则
∴
，∴为增函数 …………………………………………4分
（2）
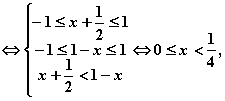………………7分
即不等式的解集为
. ……………………………………8分
（3）由于为
增函数，
∴的最大值为
对
恒成立
对
的恒成立,
设
，则
……9分
又
，
.…11分
所以实数t的取值范围为
…