（本题满分13分）
已知函数
。
（1）若函数
在
上是单调递增函数，求实数
的取值范围；
（2）求函数在上的最大值。
（本题满分13分）
已知函数。
（1）若函数在上是单调递增函数，求实数的取值范围；
（2）求函数在上的最大值。
（本题满分13分）
解：
(x)=
+a
（1）只要在x∈[0，2]上(x)≥0恒成立，
a≥
而∈[
，1]，∴a≥1 （5分）
(2)∵当x∈[0，2]时，∈[－1，－]
∴①当a≤时，(x)≤0，这时f(x)在[0，2]上单调递减，f(x)≤f(0)=1+ln3
（7分）
②当<a<1时，令(x)=0，可解得x=3－
，
∵当x∈[0，3－]时，有(x)>0
当x∈[3－，2]时，有(x)<0，
∴x=3－是f(x)在[0，2]上的唯一的极大值，
则f(x)≤f(3－)=3a－lna （10分）
③当a≥1时，(x)≥0，这时f(x)在[0，2]上单调递增，
f(x)≤f(2)=2a+1 （12分）
综上所述：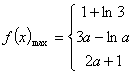
（13分）