已知数列
是公比为q的等比数列，S
是其前
项和，且S
，S
，S
成等差数列．
(1)求证：
也成等差数列．
(2)判断以为前三项的等差数列的第四项是否也是数列
中的一项，若是，求出这一项；若不是，请说明理由．
已知数列是公比为q的等比数列，S是其前项和，且S，S，S成等差数列．
(1)求证：也成等差数列．
(2)判断以为前三项的等差数列的第四项是否也是数列中的一项，若是，求出这一项；若不是，请说明理由．
解：(1)证明：若q=1，则S
，S9=9
，S6=6，而≠0，
所以S3，S9，S6不可能成等差数列，所以q≠1．
则由公式
，
得
即
，∴
，
∴2
即
成等差数列．
(2)由
得
要以为前三项的等差数列的第四项是数列
中的第
项，
必有
，所以
所以
，所以
，
所以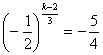
，
由是整数，所以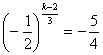不可能成立，
所以以为前三项的等差数列的第四项不可能也是数列中的一项．