(1)长轴长是短轴长的2倍,且过点(2,-6);
(2)在x轴上的一个焦点与短轴两端点的连线互相垂直,且焦距为6.
(1)长轴长是短轴长的2倍,且过点(2,-6);
(2)在x轴上的一个焦点与短轴两端点的连线互相垂直,且焦距为6.
解:(1)设椭圆的标准方程为
=1或
=1.
由已知a=2b,①
且椭圆过点(2,-6),从而有
+
=1或
=1.②
由①②得a2=148,b2=37或a2=52,b2=13,
故所求的标准方程为
+
=1或
+
=1.
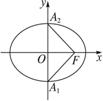
(2)如图所示,△A1FA2为一等腰直角三角形,OF为斜边A1A2的中线（高),且OF=c,A1A2=2b,
∴c=b=3,∴a2=b2+c2=18,故所求椭圆的方程为
=1.
点评:求椭圆的标准方程的一般步骤和方法是:
(1)求出基本参数a、b;
(2)确定焦点所在的坐标轴;
(3)写出标准方程.