已知函数![]() .
.
(1)当![]() 时,判断
时,判断![]() 的单调性;
的单调性;
(2)求证:![]() .
.
已知函数![]() .
.
(1)当![]() 时,判断
时,判断![]() 的单调性;
的单调性;
(2)求证:![]() .
.
解:
(1)当![]() 时,
时,![]() ,
,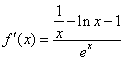
令![]() ,则
,则![]() 在
在![]() 上为减函数,且
上为减函数,且![]()
所以,当![]() 时,
时, ![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时, ![]() ,
,![]() 单调递减.
单调递减.
故![]() 递增区间为
递增区间为![]() ;
;![]() 递减区间为
递减区间为![]() …………4分
…………4分
(2)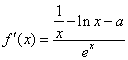 ,
,![]()
只需证![]()
即 ![]() …………6分
…………6分
易证![]() 成立. …………8分
成立. …………8分
记![]() ,则
,则![]() 令
令![]() ,得
,得![]()
并且,当![]() 时,
时,![]() ,
,![]() 单调递增;当
单调递增;当![]() 时,
时,![]() ,
,![]() 单调递减
单调递减
所以,![]()
即![]() ,命题得证. …………12分
,命题得证. …………12分