如图,在直三棱柱![]() 中,
中,![]() ,
,![]() 是棱
是棱![]() 上
上
的一点,![]() 是
是![]() 的延长线与
的延长线与![]() 的延长线的交点,且
的延长线的交点,且![]() ∥平面
∥平面![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角![]() 的平面角的正弦值.
的平面角的正弦值.
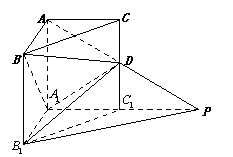
如图,在直三棱柱![]() 中,
中,![]() ,
,![]() 是棱
是棱![]() 上
上
的一点,![]() 是
是![]() 的延长线与
的延长线与![]() 的延长线的交点,且
的延长线的交点,且![]() ∥平面
∥平面![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角![]() 的平面角的正弦值.
的平面角的正弦值.

![]() 解:(Ⅰ)连接
解:(Ⅰ)连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
∵![]() ∥平面
∥平面![]() ,
,![]() 面
面![]() ,面
,面![]() 面
面![]()
![]() ∴
∴![]() ∥
∥![]() ……………2分
……………2分
又∵![]() 为
为![]() 的中点,
的中点,
∴![]() 为
为![]() 中点∴
中点∴![]() 为
为![]() 中点 ……………4分
中点 ……………4分
∴![]() ∴
∴![]() ……………5分
……………5分
(Ⅱ)∵在直三棱柱![]() 中,
中,![]()
∴![]()
![]() ……………6分
……………6分
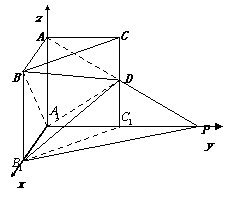
以![]() 为坐标原点,以
为坐标原点,以![]() ,
, ![]()
![]() 所在直线建立空间直角坐标系如图所示。
所在直线建立空间直角坐标系如图所示。
由(Ⅰ)知![]() 为
为![]() 中点
中点
∴点![]() 坐标分别为
坐标分别为
![]() ,
,![]() ,
,![]() ,
,![]()
![]()
设平面![]() 的法向量
的法向量![]()
∵![]() 且
且 ![]()
∴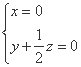 取
取![]() ∴
∴![]() ……………8
……………8![]() 分
分
同理:平面![]() 的法向量
的法向量![]() ……………10分
……………10分
设二面角![]() 平面角为
平面角为![]()
则![]() , ∴
, ∴![]() ……………12分
……………12分