设动点
到定点
的距离比它到
轴的距离大1，记点
的轨迹为曲线
.
（1）求点的轨迹方程；
（2）设圆
过
，且圆心在曲线上，
是圆在轴上截得的弦，试探究当运动时，弦长
是否为定值？为什么？
设动点到定点的距离比它到轴的距离大1，记点的轨迹为曲线.
（1）求点的轨迹方程；
（2）设圆过，且圆心在曲线上，是圆在轴上截得的弦，试探究当运动时，弦长是否为定值？为什么？
（1）曲线
方程是
（2）当
运动时，弦长
为定值4
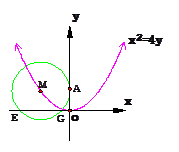
（1）依题意知，动点到定点的距离等于到直线
的距离，曲线是以原点为顶点，为焦点的抛物线………………………………2分
∵
∴
∴ 曲线方程是
………4分
（2）设圆的圆心为
，∵圆过，
∴圆的方程为 
……………………………7分
令
得：
设圆与轴的两交点分别为
，
方法1：不妨设
，由求根公式得
，
…………………………10分
∴
又∵点在抛物线上，∴
，
∴ 
，即＝4--------------------------------------------------------13分
∴当运动时，弦长为定值4…………………………………………………14分
〔方法2：∵
，
∴
又∵点在抛物线上，∴， ∴ 
∴当运动时，弦长为定值4〕