如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角的平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E,则:
1.图中有几个等腰三角形?请说明理由 。
2.BD,CE,DE之间存在着怎样的数量关系?请说明.
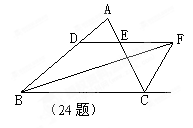
如图,∠ABC的平分线BF与△ABC中∠ACB的相邻外角的平分线CF相交于点F,过F作DF∥BC,交AB于D,交AC于E,则:
1.图中有几个等腰三角形?请说明理由 。
2.BD,CE,DE之间存在着怎样的数量关系?请说明.

1.有2个等腰三角形,分别是△BDF,△ECF
理由如下:∵ BF 平分∠ABC ∴∠ABF=∠CBF ∵ DF∥BC ∴∠DFB=∠CBF ∴∠ABF=∠DFB ∴BD=DF 即△BDF是等腰三角形
同理,△ECF是等腰三角形
2.DF=DE+EC
理由如下 :(略)
解析:略