在直角坐标系![]() 中,已知直线l1:
中,已知直线l1:![]() (
(![]() ,
,![]() ),抛物线
),抛物线
C: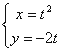 (t为参数).以原点
(t为参数).以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求直线l1 和抛物线C的极坐标方程;
(Ⅱ)若直线l1 和抛物线C相交于点A(异于原点O),过原点作与l1垂直的直线l2,l2和抛物线C相交于点B(异于原点O),求△OAB的面积的最小值.
在直角坐标系![]() 中,已知直线l1:
中,已知直线l1:![]() (
(![]() ,
,![]() ),抛物线
),抛物线
C: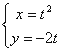 (t为参数).以原点
(t为参数).以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求直线l1 和抛物线C的极坐标方程;
(Ⅱ)若直线l1 和抛物线C相交于点A(异于原点O),过原点作与l1垂直的直线l2,l2和抛物线C相交于点B(异于原点O),求△OAB的面积的最小值.
解:(Ⅰ)可知l1是过原点且倾斜角为![]() 的直线,其极坐标方程为
的直线,其极坐标方程为
![]()
![]()
抛物线C的普通方程为![]() ,
,
其极坐标方程为![]() ,
,
化简得![]() .
.
(Ⅱ)解法1:由直线l1 和抛物线C有两个交点知![]() ,
,
把![]() 代入
代入![]() ,得
,得![]() ,-----------------6分
,-----------------6分
可知直线l2的极坐标方程为![]()
![]() ,-----------------------7分
,-----------------------7分
代入![]() ,得
,得![]() ,所以
,所以![]() ,----8分
,----8分
![]()
![]()
![]() ,
,
∴△OAB的面积的最小值为16.
【解法2:设![]() 的方程为
的方程为![]() ,由
,由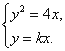 得点
得点![]() ,------6分
,------6分
依题意得直线![]() 的方程为
的方程为![]() ,同理可得点
,同理可得点![]() ,-------------7分
,-------------7分
故![]() -------------------------8分
-------------------------8分
![]() ,(当且仅当
,(当且仅当![]() 时,等号成立)
时,等号成立)
∴△OAB的面积的最小值为16.B