(1)若从A、B两市各调x台到D市,当三市28台机器全部调运完毕后,求总运费P(x)关于x的函数表达式,并求出P(x)的最大值和最小值;
(2)若从A市调x台到D市,从B市调y台到D市,当28台机器全部调运完毕后,用x、y表示总运费P,并求P的最大值和最小值.
(1)若从A、B两市各调x台到D市,当三市28台机器全部调运完毕后,求总运费P(x)关于x的函数表达式,并求出P(x)的最大值和最小值;
(2)若从A市调x台到D市,从B市调y台到D市,当28台机器全部调运完毕后,用x、y表示总运费P,并求P的最大值和最小值.
(1)P(x)=17 200-800x(5≤x≤9),
P(x)max=13 200(元),
P(x)min=10 000(元).
(2)Pmax=14 200(元),
Pmin=9 800(元).
解析:(1)
运量需方 | A | B | C | 需量 |
D | x | x | 18-2x | 18 |
E | 10-x | 10-x | 2x-10 | 10 |
供量 | 10 | 10 | 8 |
|
2x≤18,x≤9,2|10-x|≤10,x≥5,
∴5≤x≤9.
∴P(x)=200x+800(10-x)+300x+700(10-x)+400(18-2x)+500(2x-10)=17 200-800x(5≤x≤9).
∴x=5时,P(x)max=13 200(元);
x=9时,P(x)min=10 000(元).
(2)
运量需方 | A | B | C | 需量 |
D | x | y | 18-x-y | 18 |
E | 10-x | 10-y | x+y-10 | 10 |
供量 | 10 | 10 | 8 |
|
x+y≤18,10-x+10-y≤10,
∴x+y≥10.
P=200x+800(10-x)+300y+700(10-y)+400(18-x-y)+500(x+y-10)=17 200-(500x+300y).
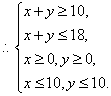
设t=500x+300y→y=![]()
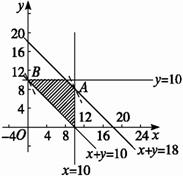
∴![]() 即为动直线在y轴上的截距.
即为动直线在y轴上的截距.
将直线在可行域内移动,可知A点处截距最大,B点处截距最小.
∵A(10,8),B(0,10),
∴Pmin=17 200-(500×10+300×8)=9 800(元),
Pmax=17 200-(300×10+0)=14 200(元).