在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,底面
,底面![]() 是梯形,
是梯形,![]()
![]() ∥
∥![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)设![]() 为棱
为棱![]() 上一点,
上一点,![]() ,
,
试确定![]() 的值使得二面角
的值使得二面角![]() 为
为![]() .
.

在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,底面
,底面![]() 是梯形,
是梯形,![]()
![]() ∥
∥![]() ,
,![]() ,
,![]() .
.
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)设![]() 为棱
为棱![]() 上一点,
上一点,![]() ,
,
试确定![]() 的值使得二面角
的值使得二面角![]() 为
为![]() .
.

【解析】![]() (Ⅰ)∵
(Ⅰ)∵![]() 平面
平面![]() ,∴
,∴![]() ,
,
 如图,在梯形
如图,在梯形![]() 中,过点
中,过点![]() 作
作![]() 于
于![]() ,则
,则![]() ,∴
,∴![]() ,
,
∵![]() , ∴
, ∴![]() , ∴
, ∴![]() ,
,
∴![]() . ∴
. ∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() 平面
平面![]() , ∴
, ∴![]() ,
,
又∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
又∵![]() 平面
平面![]() , ∴平面
, ∴平面![]() 平面
平面![]() .
.
 (Ⅱ)法一:过点
(Ⅱ)法一:过点![]() 作
作![]() ∥
∥![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连
,连![]() ,
,
由(Ⅰ)可知![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴![]() ,∵
,∵![]() ,
,
∴![]() 平面
平面![]() ,∴
,∴![]() ,
,
∴![]() 是二面角
是二面角![]() 的平面角,
的平面角,
∴![]() ,∵
,∵![]() , ∴
, ∴![]() ,
,
∵![]() ∥
∥![]() , ∴
, ∴![]() ,
,
∴![]() ,由(Ⅰ)知
,由(Ⅰ)知![]() ,∴
,∴![]() , 又∵
, 又∵![]() ,
,![]() ∥
∥![]() ,
,
∴![]() , ∴
, ∴![]() ,
,
∵![]() ,∴
,∴![]()
![]() .
.
 法二:以
法二:以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() 轴建立空间直角坐标系(如图), 则
轴建立空间直角坐标系(如图), 则![]() ,
,![]() ,
,![]() ,
,![]() ,令
,令![]() ,
,
则![]() ,
,![]() ,
,
∵![]() , ∴
, ∴![]() ,
,
∴![]() ,
,![]()
![]() ∵
∵![]() 平面
平面![]() ,
,
∴![]() 是平面
是平面![]() 的一个法向量,设平面
的一个法向量,设平面![]()
![]() 的法向量为
的法向量为![]() ,则
,则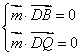 ,即
,即 ![]() 即
即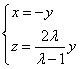 ,
,
不妨令![]() ,得
,得![]() ,
,
∵二面角![]() 为
为![]() ,∴
,∴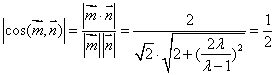 ,
,
解得![]() , ∵
, ∵![]() 在棱
在棱![]() 上, ∴
上, ∴![]() , ∴
, ∴![]() .
.