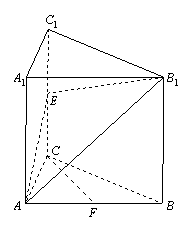
 如图,已知直三棱柱
如图,已知直三棱柱![]() ,
,![]() ,
,![]() ,
,![]() .
.![]() 、
、![]() 分别是棱
分别是棱![]() 、
、![]() 中点.
中点.
⑴ 求证:![]()
![]() ; ⑵求四棱锥
; ⑵求四棱锥![]() 的体积;
的体积;
⑶ 判断直线![]() 和平面
和平面![]() 的位置关系,并加以证明.
的位置关系,并加以证明.
 如图,已知直三棱柱
如图,已知直三棱柱![]() ,
,![]() ,
,![]() ,
,![]() .
.![]() 、
、![]() 分别是棱
分别是棱![]() 、
、![]() 中点.
中点.
⑴ 求证:![]()
![]() ; ⑵求四棱锥
; ⑵求四棱锥![]() 的体积;
的体积;
⑶ 判断直线![]() 和平面
和平面![]() 的位置关系,并加以证明.
的位置关系,并加以证明.
⑴∵三棱柱![]() 是直棱柱,∴
是直棱柱,∴![]() 平面
平面![]() .
.
又∵![]() 平面
平面![]() , ∴
, ∴![]()
![]() .
.
⑵解:∵三棱柱![]() 是直棱柱,
是直棱柱,
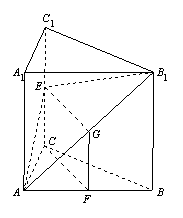 ∴
∴![]() 平面
平面![]() .
.
又∵![]() 平面
平面![]() ,∴
,∴![]()
![]() .
.
∵![]() ,∴
,∴![]()
![]() .
.
∵![]()
![]()
![]() ,∴
,∴![]()
![]() 平面
平面![]() .
.
∴![]() .
.
∵![]() 是棱
是棱![]() 的中点,∴
的中点,∴![]() .
.
∴![]() .
.
∴![]() .
.
⑶解:![]() 平面
平面![]() .证明如下:取
.证明如下:取![]() 的中点
的中点![]() ,联结
,联结![]() ,
,![]() .
.
∵![]() 、
、![]() 分别是棱
分别是棱![]() 、
、![]() 中点,∴
中点,∴![]() ,
,![]()
![]() .
.
又∵![]() ,
,![]() ,∴
,∴![]() ,
,![]() .
.
∴四边形![]() 是平行四边形, ∴
是平行四边形, ∴![]() ∥
∥![]() .
.
又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() , ∴
, ∴![]() 平面
平面![]() .
.