如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥上底面ABC,AB=AC=2AA1,∠ABC=30°,D,D1分别是线段BC,B1C1的中点,M是线段AD的中点.
(1)在平面ABC内,试作出过点M与平面A1BC平行的直线l,说明理由,并证明直线l⊥平面ADD1A1;
(2)设(1)中的直线l交AB于点P,交AC于点Q,求二面角A-A1P-Q的余弦值.
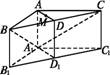
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥上底面ABC,AB=AC=2AA1,∠ABC=30°,D,D1分别是线段BC,B1C1的中点,M是线段AD的中点.
(1)在平面ABC内,试作出过点M与平面A1BC平行的直线l,说明理由,并证明直线l⊥平面ADD1A1;
(2)设(1)中的直线l交AB于点P,交AC于点Q,求二面角A-A1P-Q的余弦值.

.解
(1)在平面ABC内,过点M作直线l∥BC.
∵l⊄平面A1BC,BC⊂平面A1BC, 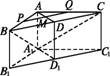
∴l∥平面A1BC.
∵AB=AC,D是BC的中点,
∴BC⊥AD.∴l⊥AD.
∵AA1⊥平面ABC,l⊂平面ABC,
∴AA1⊥l.
又AD⊂平面ADD1A1,AA1⊂平面ADD1A1,且AD∩AA1=A,∴l⊥平面ADD1A1.
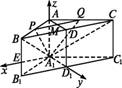
(2)设AA1=1,如图,过A1作A1E∥B1C1,以A1为坐标原点,分别以A1E,A1D1,A1A所在直线为x轴、y轴、z轴建立空间直角坐标系.
则A1(0,0,0),A(0,0,1),B(,1,1),C(-,1,1).∵M为线段AD的中点,∴P,Q分别为AB,AC的中点.
∴P,Q,
=(0,0,1),=(,0,0).
设平面AA1P的一个法向量为n1=(x1,y1,z1),则
即
令x1=1,则y1=-,于是n1=(1,-,0).
设平面A1PQ的一个法向量为n2=(x2,y2,z2),则
即
令y2=2,则z2=-1,于是n2=(0,2,-1).
设二面角A-A1P-Q的平面角为θ,又θ为锐角,则cos θ=
故二面角A-A1P-Q的余弦值为