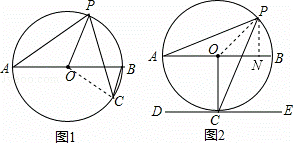
在⊙O中，AB为直径，PC为弦，且PA=PC
（1）如图1，求证：OP∥BC
（2）如图2，DE切⊙O于点C，DE∥AB，求tan∠A的值．
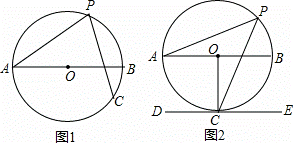
在⊙O中，AB为直径，PC为弦，且PA=PC
（1）如图1，求证：OP∥BC
（2）如图2，DE切⊙O于点C，DE∥AB，求tan∠A的值．
证明：（1）连接OC．
∵PA=PC
∴弧PA=弧PC，
∴∠AOP=∠COP，
∵OA=OP，
∴∠A=∠APO，
同理，∠PCO=∠CPO，
∴∠A=∠CPO，
∵∠A=∠BCP，
∴∠BCP=∠CPO，
∴BC∥OP；
（2）连接OP，过P作PN⊥AB于点N．
∵DE为⊙O的切线，
∴OC⊥DE，
∴∠DCO=90°，
∵AB∥DE，
∴∠AOC+∠DCO=180°，
∴∠AOC=90°，
∴∠AOP=∠COP=135°．
∵∠AOP+∠BOP=180°，
∴∠BOP=45°，
∵PN⊥AB，
∴ON=PN=
OP，
∵AO=PO，
∴AN=（1+）OP，
∴tanA=
=
=
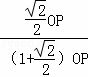﹣1．
