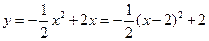（2011内蒙古赤峰，25，14分）如图（图1、图2），四边形ABCD是边长为4
（2011内蒙古赤峰，25，14分）如图（图1、图2），四边形ABCD是边长为4的正方形，点E在线段BC上，∠AEF=90°，且EF交正方形外角平分线CP于点F，FN⊥BC，交BC的延长线于点N。
（1）若点E是BC的中点（如图1），AE与EF相等吗？为什么？
（2）点E在BC间运动时（如图2），设BE=x,△ECF的面积为y。
①求y与x的函数关系式；
②当x取何值时，y有最大值，并求出这个最大值。
解：（1）相等。
理由：∵四边形ABCD是正方形，点E是BC的中点
∴∠B=∠DCN="90°." AB=BC=2BE，
∴∠BAE+∠BEA=90°.
∵∠AEF=90°
∴∠AEB+∠FEC=90°.，
∴∠BAE=∠FEN.
∵CF是∠DCN的角平分线，∠FNC=90°。
∴∠FCN=∠CFN=45°.
∴FN=CN.
在Rt△ABE和Rt△ENF中
∴EN=2FN，∴EC＋CN=2CN，∴FN="BE" .
∴Rt△ABE≌Rt△ENF.
∴AE=EF.
方法二：如图，取AB的中点M，连结ME.
∵四边形ABCD是正方形，
∴AB=BC，∠B=∠DCN=90°，
∵点E是BC的中点
∴AM=MB=BE=EC
在Rt△MBE中，∠BME=∠BEM=45°.
∴∠AME=135°；
∵CF是∠DCN的角平分线，
∴∠FCN=45°.
∴∠ECF=135°.
∴∠AME="∠ECF" ；
∵∠AEF="90° " ；
∴∠AEB+∠FEC="90°" ；
在Rt△ABE中，∠BAE+∠AEB=90°.
∴∠BAE="∠FEN " ；
∴△AME≌△ECF ；
∴AE="EF" 。
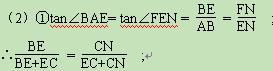
∴BE(EC+CN)="CN(BE+EC)" ;
∴BE·EC＋ BE·CN =" BE·CN" ＋CN·EC ;
∴BE·EC =" CN·EC" ;
∴BE =" CN " ;
∴BE ="FN" =" x" ，
∴
。
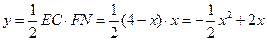
②
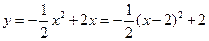
当x =2时，y有最大值为2.解析:
略
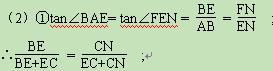
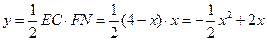