如图，把矩形纸片OABC放入平面直角坐标系中，使OA、OC分别落在x轴、y轴上，连接OB，将纸片OABC沿OB折叠，使点A落在点A′的位置，若OB＝
，tan∠BOC＝
，则点A′的坐标为 ．
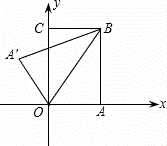
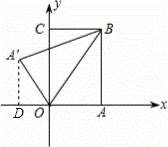
如图，把矩形纸片OABC放入平面直角坐标系中，使OA、OC分别落在x轴、y轴上，连接OB，将纸片OABC沿OB折叠，使点A落在点A′的位置，若OB＝，tan∠BOC＝，则点A′的坐标为 ．
（
，
）
解析：如图，过点A′作A′D⊥x轴与点D；设A′D＝λ，OD＝μ；∵四边形ABCO为矩形，
∴∠OAB＝∠OCB＝90°；四边形ABA′D为梯形；设AB＝OC＝γ，BC＝AO＝ρ；
∵OB＝
，tan∠BOC＝
，∴
，解得：γ＝2，ρ＝1；
由题意得：A′O＝AO＝1；△ABO≌△A′BO；由勾股定理得：λ2+μ2＝1①，
由面积公式得：
②；
联立①②并解得：λ＝，μ＝
．故答案为（，）．