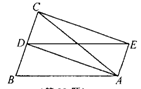
已知:如图,△ABC中,AD是BC边上的中线,四边形ABDE是平行四边形(1
已知:如图,△
ABC中,
AD是
BC边上的中线,四边形
ABDE是平行四边形
(1)求证:四边形
ADCE是平行四边形;
(2)当△
ABC满足什么条件时,四边形
ADCE是菱形?说明你的理由.
(1)见解析(2)当△ABC满足∠BAC=90°时,四边形ADCE是菱形,理由见解析解析:
(1)证明:∵四边形ABDE是平行四边形,
∴BD∥AE,BD=AE. …………………………1分
∵△ABC中,AD是BC边上的中线
∴BD=CD.
∴CD=AE. …………………………2分
又∵CD∥AE,∴四边形ADCE是平行四边形. ………3分
(2)解:当△ABC满足∠BAC=90°时,四边形ADCE是菱形.……………………4分
∵△ABC中,∠BAC=90°,BD=CD.
∴AD=CD. ……………………5分
又∵四边形ADCE是平行四边形,
∴四边形ADCE是菱形. ……………………6分
证明是平行四边形的方法有很多,此题用一组对边平行且相等较为简单,在平行四边形的基础上只需邻边相等即可证出菱形

